今年的ILSVRC的DET和LOC比赛都被MSRA拔得头筹，其中DET的mean AP比第二名高了近9％，研究工作有两篇论文：
- Deep Residual Learning for Image Recognition
- Instance-aware Semantic Segmentation via Multi-task Network Cascades
PS.因为实习和学校里的事情，好久没认真研究论文，写论文笔记了
首先看Residual Network ## Motivation - Degradation problem: Training Error increases with the network gets deeper - If the added layers can be constructed as identity mappings，a deeper model should produce no higher training error than its shallower counterpart 如果我们增加层数之后可以做到全等映射的话，那么对于更深的网络，training error不可能比shallow的更高，我们知道单隐层的神经网络是可以无限逼近任何一个非线性函数的，因此训练全等映射是可行的。
作者指出，比起重头开始训练一个全等映射，我们尝试在原始输入上添加一个小的扰动（噪声），通过将扰动最小化让它逼近0来做到全等映射更加容易一些，这也就是residual learning的概念
Deep Residual Learning
我们把degradation问题视作一个优化问题，为了解决这个问题，作者将原先的层与层之间的映射转化成两部分： * 与输入相同的Identity mapping * 输入与原先输出部分的残余Residual mapping 体现在神经网络的结构上如下图: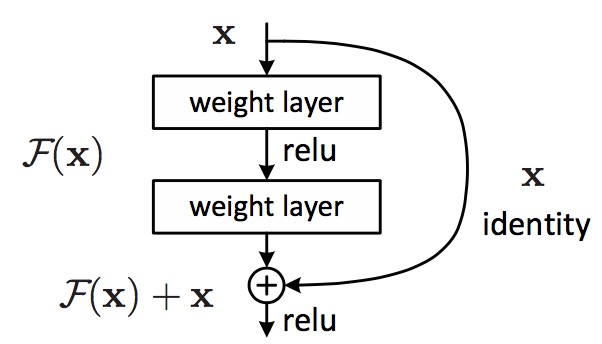 
这个概念是整篇文章的核心，图中x表示输入，$ H(x) ＝ F(x) + x\(， 式中\)H\(就是原先的mapping函数，\) F$和x分别代表Residual mapping和Identity mapping.该结构不仅仅适用于全连接层，卷积层同样也适用。
图中identity映射部分叫做shortcut，这里我们可以不加参数使其完全等于输入x，或者我们也可以添加权重使identity变为projection，将identity转化为projection的做法主要是为了解决经过卷积层后输入与输出维度不同的问题。
同时我们注意到如果是identity全等映射，那么这里没有任何需要训练的参数，因此一个block的参数数量与普通的神经网络相同，这对于训练速度是非常大的帮助。
Advantages of Residual Learning
- Easy to optimize, converge fast
- Small number of parameters
- Accuracy gains from greatly increased depth 笔者认为Residual learning最大的好处在于降低了设计deep neural network网络结构的难度，过去在设计网络时我们很难想象当网络达到几十层甚至上百层之后对网络的性能会有多大的负面影响，因此为了避免非常深的网络，转而通过增加网络宽度，或者引入其他的算法来改进网络结构，但是引入residual之后，仅仅是将网络加深却能得到非常好的效果，可以预见到16年的CV必然会有非常大的突破
笔者个人猜测：可能引入residual之后原先的优化问题中local minimal会少很多，使得优化过程更加容易到达global minimal或者比较好的local minimal，同时residual部分的值都非常小，因此相对而言在BP过程中梯度不会小到接近vanish的状态。 同时这里有一个细节，训练时并没有使用dropout来避免过拟合，但是最后结果也令人非常满意
Details
Shortcut Options
前面提到过identity部分可以转化为projection，作者在这里给出了三种方案： * (A) zero-padding shortcuts are used for increasing dimensions * (B) projec- tion shortcuts are used for increasing dimensions, and other shortcuts are identity * (C) all shortcuts are projections. 实验结果证明三种方案都能提升效果，但是C引入了更多的参数，而实际效果并没有比A和B好多少，但是训练时间和成本却高得多，因此前两种方案比较可行。
Layer Responses
实验过程中经过观察发现residual部分的输出值缺失非常接近0，验证了开头的设想，同时增加网络深度之后，residual的值变得更小，说明了这样的网络结构能很好地解决degredation的问题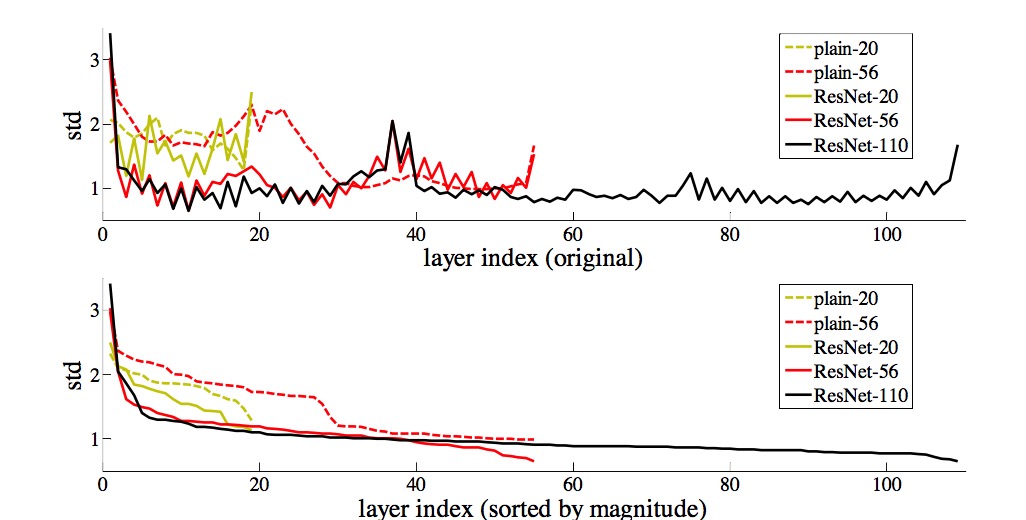 
总体而言文章通过实验验证experimental insight不多，但是使用了非常浅显易懂的方式成功解决了深度神经网络的热点问题，对于deep learning而言着实是非常大的进步。值得注意的是related work中提到了highway network，与本文的思想非常接近，有空又得读了……
下面是第二篇Instance-aware Semantic Segmentation via Multi-task Network Cascades ## Multi-task Network Cascades abstract中就已经提到三个网络级联构成一个新的框架 instance-aware semantic segmentation task can be decomposed into three sub-tasks
- Differentiating instances —— Bounding box indicating instances
- Estimating masks —— pixel-level mask
- Categorizing objects —— category-wise label
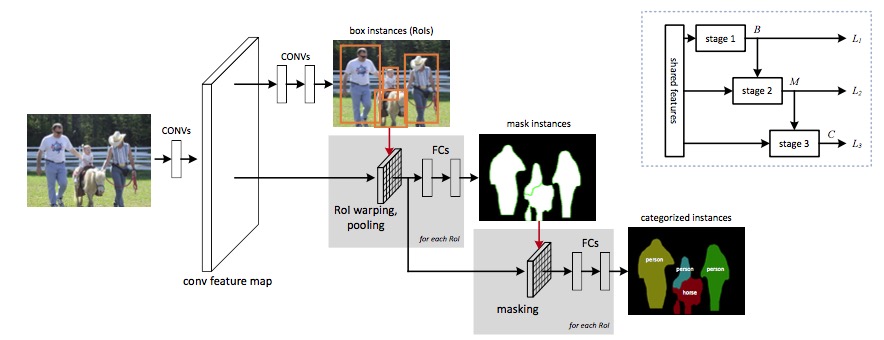
三个子任务共享卷积网络的feature，但是后面的任务接受feature和前一个任务的输出作为输入。 整个框架其实是首先用bounding box框出instance(类似于RPN)，之后在每个bounding box中生成pixel wise的mask，最后给每个instance分类
本文中使用了ResNet来提取feature
Regressing Box-level Instances 做法类似于RPN，给定一副图像输出含有instance的bbox，稍有不同的是本文中使用了\(1\times1\) 的convolutional layer做box regression和object classifying
Regressing Mask-level Instances 借助Fast RCNN中的Roi pooling，在第二阶段对每个ROI生成相同维度的feature，后面再接两个fc层，一个降维到256，另一个做pixel－wise regression,
值得一提的是到这一步Loss function需要修改，由于第二部的结果依赖于第一步的输出，因此该步骤的Loss function为: \[L_2 = L_2(M(\theta) | B(\theta))\]
\(B(\theta))\)表示第一阶段用于生成bounding box的参数，M()表示用于生成mask的参数
- Categorizing Instances 到了第三步，我们接收第二步的feature对每个mask重新计算feature： \[\mathcal F_i^{Mask}(\theta) = \mathcal F_i^{RoI}(\theta) \cdot M_i(\theta)\]
\(M_i(\theta)\)表示第二步输出的mask，\(\mathcal F_i^{RoI}\)就是经过RoI pooling的feature map，做点乘得到Mask的feature，后面接两个4096维的fc层，这被称为mask-based pathway, 类似的对RoI pooling输出的feature也做相同的处理,即box-based pathway, 这两个pathway的输出连接起来feed到softmax中进行分类
同样，第三阶段的Loss function计算公式为: \[L_3 = L_3(C(\theta) | M(\theta), B(\theta))\]
Training Method
整个网络结构梳理完毕，三个阶段的Loss function相加就可以得到总的损失函数，但是由于参数之间的依赖性，BP的时候第一阶段Bounding box的梯度传播是个比较大的难题。
对比Fast RCNN， 用Selective Search生成的RoI在训练网络时是固定的，并且又不能像RPN那样直接对bbox regression的Loss做反向传播（因为bbox只是中间过程的输出而已），为此作者提出可以求导的RoI Warping Layers来将残差传递给bounding box层。
replace the RoI pooling layer with a RoI warping layer followed by a maxpooling layer
RoI Warping Layer
Crops a feature map region and warps it into a target size by interpolation 显然，在RoI pooling层前面添加一层warping layer, 每个RoI都被crop和warp到固定size(在本文中大小为28 \(\times\) 28),转化方法如下： \[ \mathcal {F_{i}^{RoI}}_{(u^\prime,v^\prime)} = \sum_{(u,v)}^{W \times H} G(u,v;u^\prime, v^\prime|B_i) \mathcal F_(u,v)\]
式中\((u,v)\)以及\((u^\prime, v^\prime)\)分别表示warp之前和warp之后feature map的元素位置，函数G是长度和宽度两个方向的双线性插值函数乘积，如此一来，Bounding box阶段的参数导数计算如下:
\[{\partial L_2 \over {\partial B_i}}= {\partial L_2 \over {\partial \mathcal F_i^{RoI}}} {\partial G \over \partial B_i} \mathcal F\]
More Stages
At stage three, ddd 4(N+1)-d fc layer for regression class-wise bounding boxes, train the bbox regression jointly with classifier.
At inference step, extend three stages to five stages 利用第三步的结果（bounding box）再运行一次相同的Mask predict和classification的过程，实验结果证明精度上升
- First run entire 3-stage network and obtain regressed boxes on stage 3, consider these boxes as new proposals
- Perform stage2 and stage3 again and the whole procedure becomes 5-stage cascading
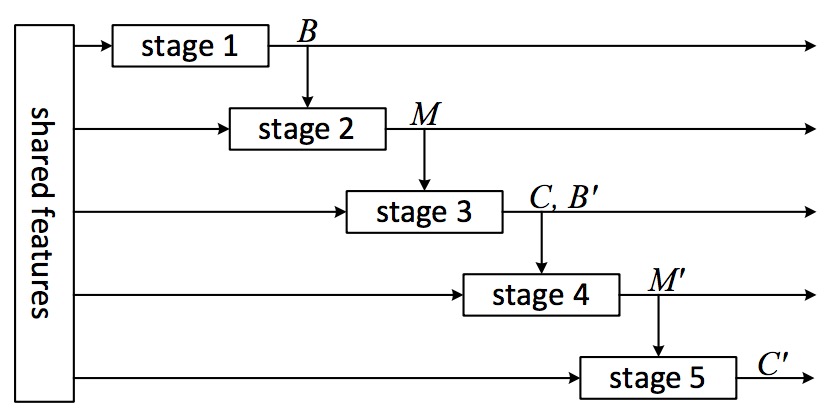
Contributions
- Joint training for semantic segmentation and object detection
- Combination of the basic concept of state-of-the-art models(FCN, Fast RCNN, RPN, Spatial Transformation Network) and improvements of Fast RCNN and RPN
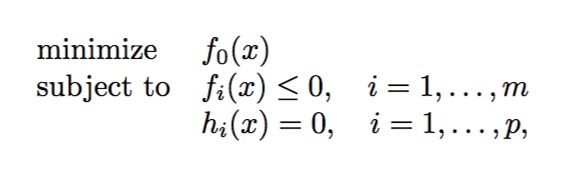
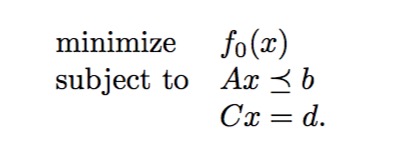
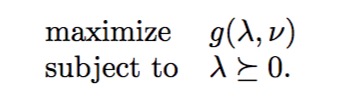前面讲过对偶函数定义了原始问题可行解的下界，那么对偶问题的目标就是试图从找到这些下界的最大值，当然我们前面已经假设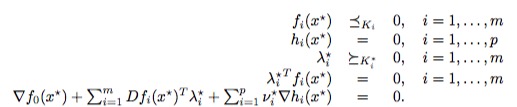
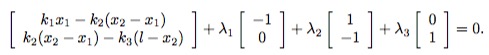
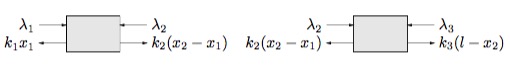动手写一下受力平衡方程就可以发现与上面的梯度为0的式子是一样的，说明了Lagrange乘子可以看作是题目中滑块受到的反作用力，KKT条件与平衡状态的受力分析殊途同归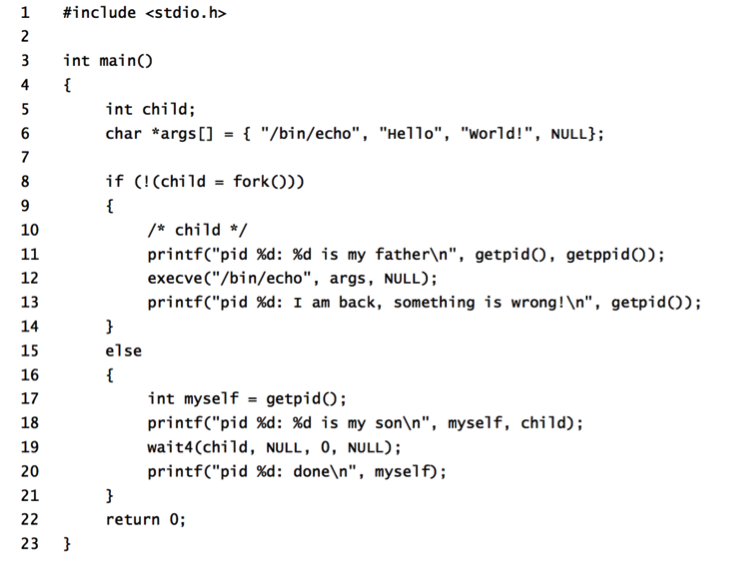
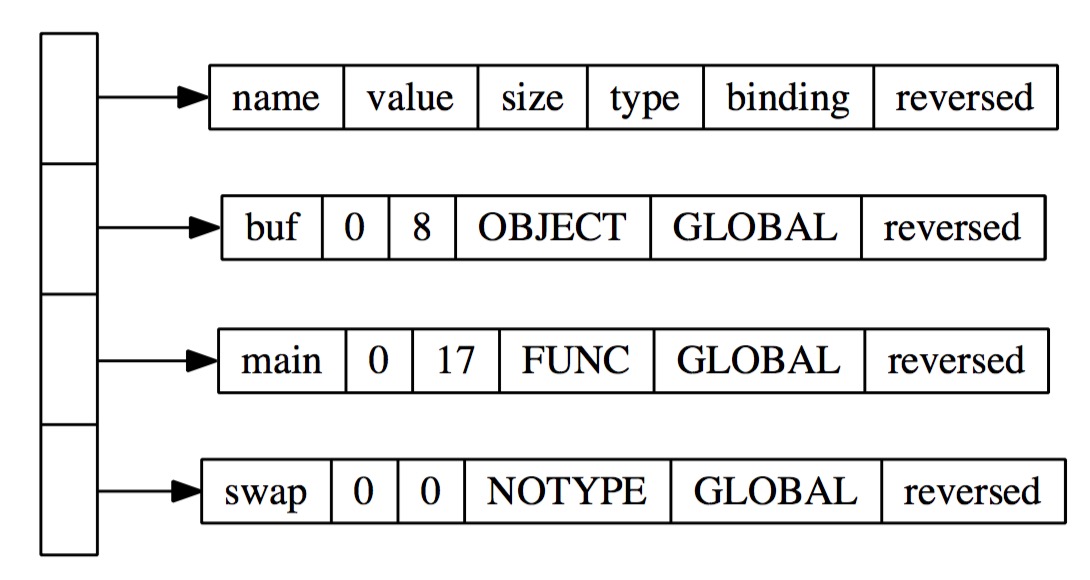
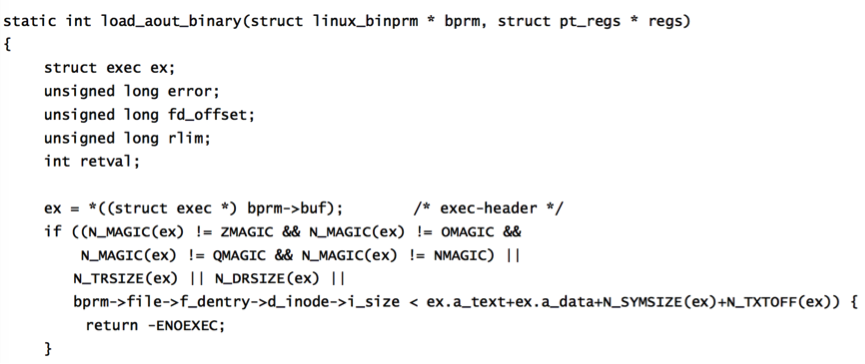回忆一下bprm中包含了装载所需要的参数，其中就包括文件类型，代码里面ex变量是一个exec数据结构，该结构中包含着文件的MagicNumber， 这里需要介绍一下MagicNumber的概念：
通过上面的分析，我们可以得出如果子进程与父进程共享用户空间，那么其实也就没有释放用户空间这一说了，但此时需要为子进程分配一个mm_struct数据结构以及页面目录，以便于为子进程建立自己的用户空间，之后切换到新的用户空间。
首先get_user是一个宏定义，用于从用户空间读取简单类型的变量，如一个字节，短整数和长整数，那么为什么要用x而不是x的地址呢？ get_user中实际调用的是__get_user_x这个汇编函数，该函数只有一条汇编指令，该指令执行以下操作：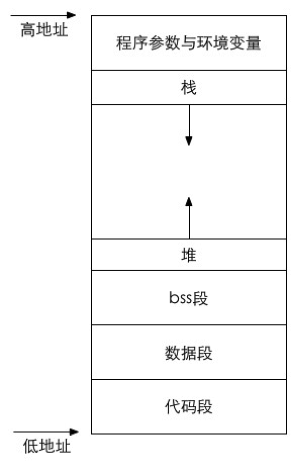
Linux系统中进程的创建分为两步：首先从父进程“派生”出一个子进程，之后子进程通过系统调用execve()执行目标程序。 在正式开始进程创建的过程之前，我们首先要了解一下Linux系统与进程密切相关的数据结构，如PCB的数据结构task_struct（后面直接用PCB表示task_struct结构），以及虚拟内存的描述符mm，这些会为之后的代码阅读与理解提供很大的便利。
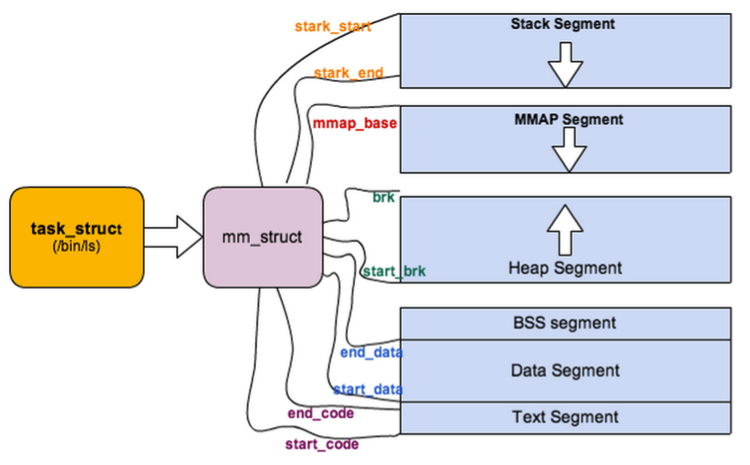共分四个段：代码段、数据段、堆和栈，进程创建时对mm_struct的复制是重点。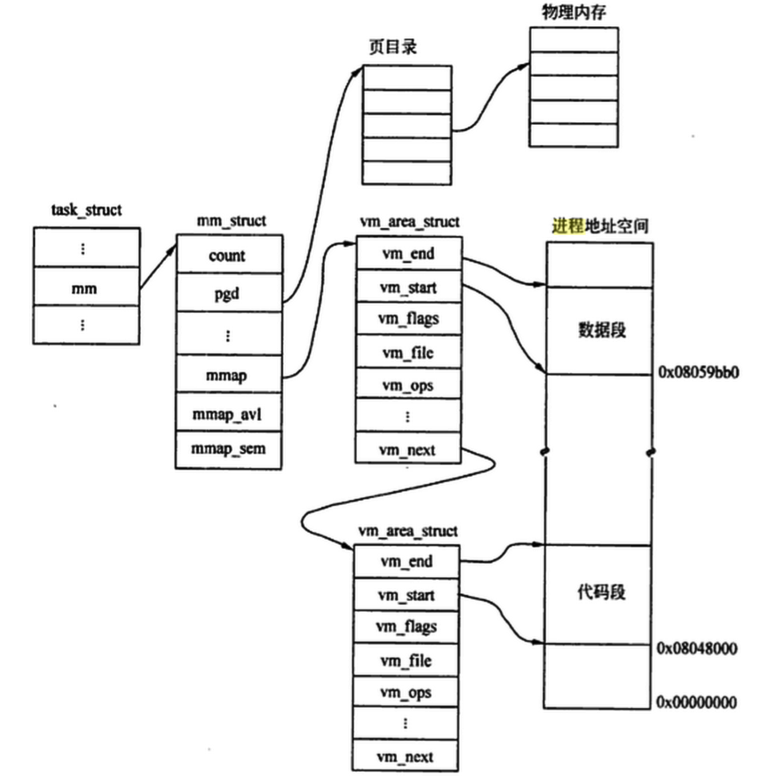
注意到其中有一个count变量，说明子进程可以通过指针共享这个信号表，只需要将共享计数加一就可以了
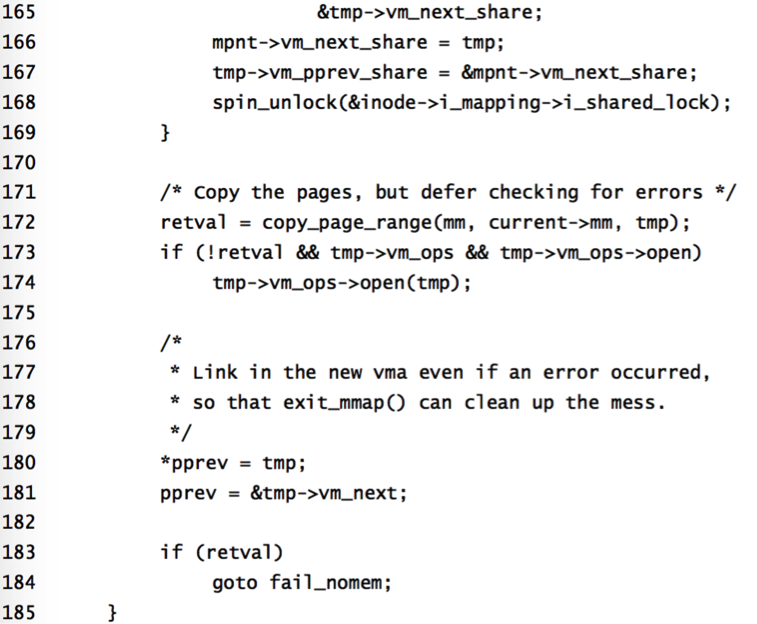函数的主题在于这个for循环当中，我们遍历当前进程mm指针的每块虚拟内存，新建一块内容空间tmp，并将其独占（变为临界资源），之后把tmp的vm_mm指向当前进程的mm字段，递增共享计数，155到169针对打开文件的处理，之后完成页面的复制，copy_page_range是一个非常关键的函数，其代码比较长，这里主要讲一下函数的执行过程
系统堆栈的内容包含了父进程从通过系统调用进入系统空间开始到进入copy_thread的过程，而子进程返回时需要这些信息，但是不能完全照搬，因为返回时我们要区分是哪个进程返回的。我们已经知道当进程通过系统调用进入内核态时，我们需要保存CPU上下文，pt_regs就是用来存储寄存器内容的数据结构，在创建pt_reg时参考下图：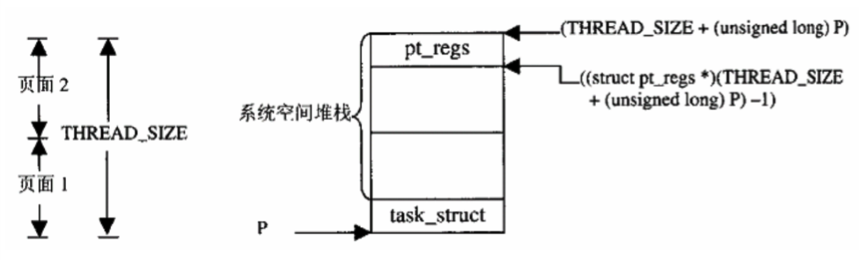 
首先我们已经有指向子进程PCB的指针p，同时我们也知道p指向两个连续的物理页面，因此我们可以得到这两个页面的顶端THREAD_SIZE+(unsigned long)p，之后将其转换为struct pt_regs*，再减一就指向了子进程系统堆栈的pt_regs结构。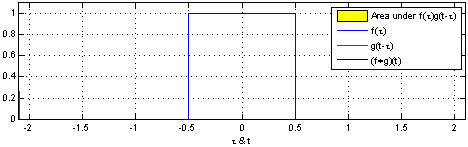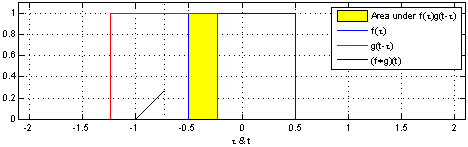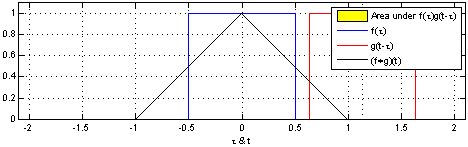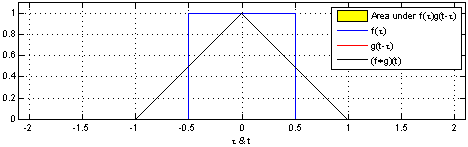
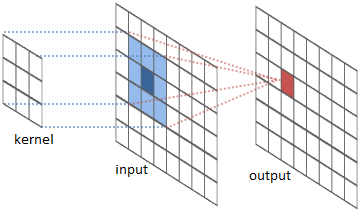
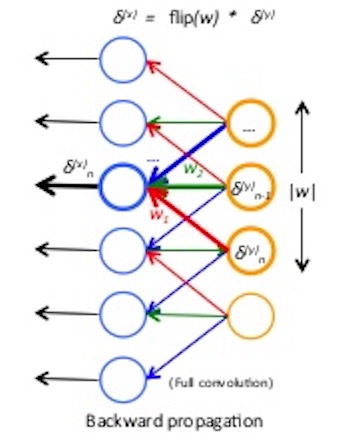
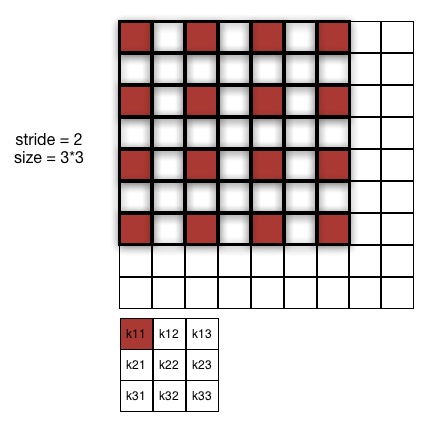
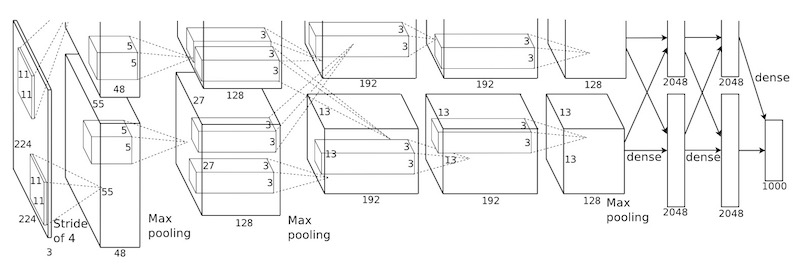
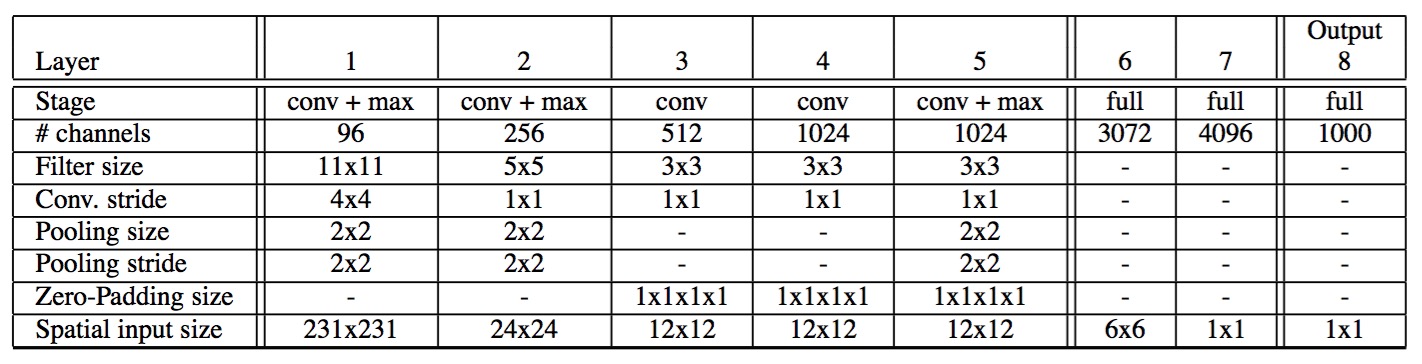
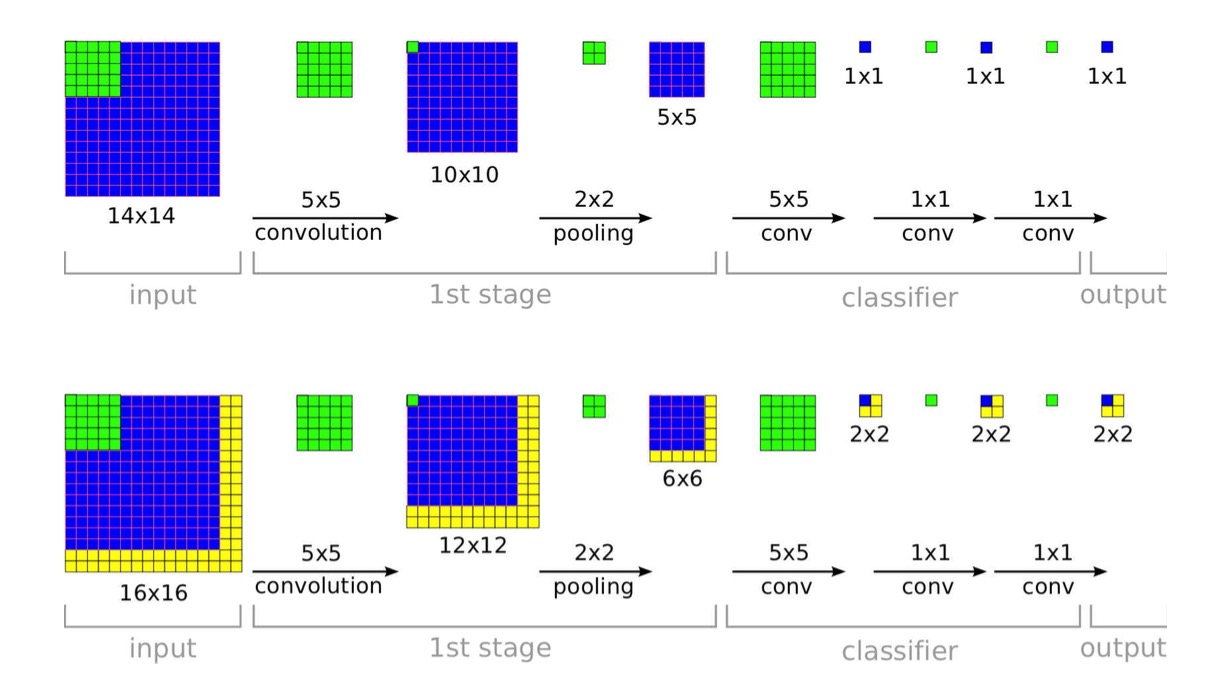
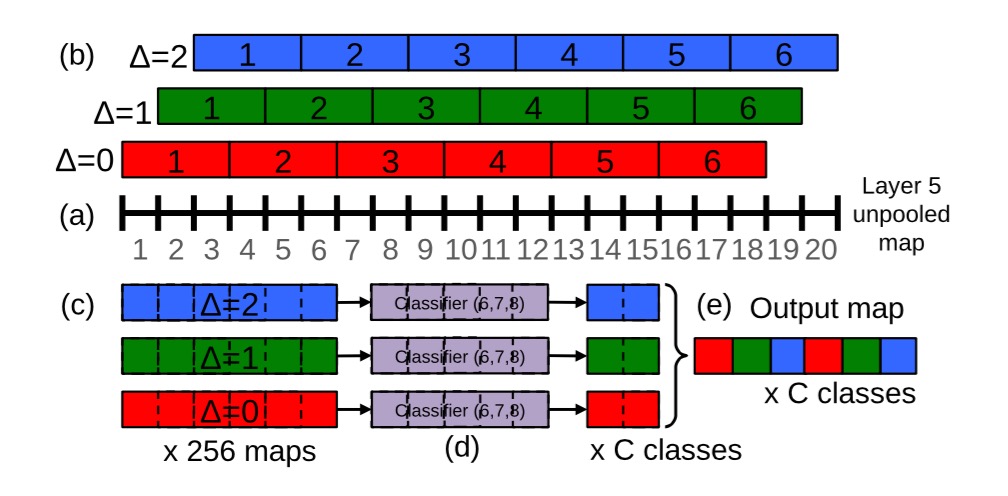按照笔者理解，原始的3*3pooling的起始位置为(0,1,2),其实就是使用stride步长为1的pooling层，之后按照原始stride进行分组，得到多个分组的pooling向量之后使用滑动窗口的方式得到feature map，重新将原先分组的结果合并成一个向量作为整张图片的feature map,无论图像的尺寸多大，使用stride为1的pooling层能最大程度上保持原始信息，并且分组之后每一个feature map向量长度保持一致。